读论文 Operational Transformation in Real-Time Group Editors

预备内容

Definition1 : Causal ordering relation -> Given two operations Oa and Ob, generated at sites i and j, then Oa -> Ob, iff: 1) i = j, and the generation of Oa happened before the generation of Ob, or 2) i != j, and the execution of Oa at site j happened before the generation of Ob, or 3) there exists an operation Ox, such that Oa -> Ox, and Ox -> Ob

这一套定义实际来自 Lamport Clock，论文名：Time, Clocks, and the Ordering of Events in a Distributed System。第一条好理解，第二条意思是说如果 Oa Ob 发生在不同的 site i 和 j。那只有当 Oa 在 j 这个 site 执行时间点早于 Ob 时，才有 Oa -> Ob。

Definition 2: Dependent and independent operations Given any two operations Oa and Ob. 1) Ob is dependent on Oa iff Oa -> Ob 2) Oa and Ob are independent (or concurrent), expressed as Oa || Ob, iff neither Oa -> Ob, nor Ob -> Oa.

例如下图，称为图 1。O1 ~ O4 是四次 Operation。Site 是 Operation 发起和执行者。

8DE0AD9D-4EDE-4AD1-BA73-CB8BBFEE9D48-61185-000056D044AC3130

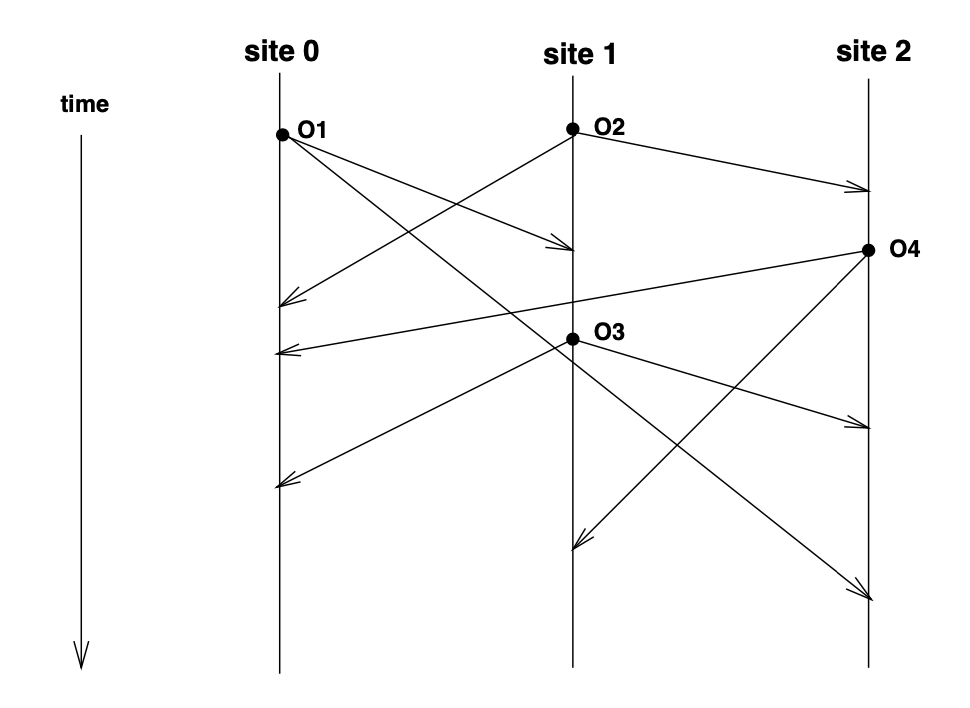
由之前 Definition 1，有 O1 -> O3, O2 -> O3, O2 -> O4，即这几个事件之间有 Happens before 关系. 按 Definition 1 也称为有 Causal Order。

由之前 Definition 2 有 O1 || O2, O1 || O4, O3 || O4，即这几个 Operation 是独立的。没有 Happens before 或 Causal order。

GROVE

GROVE 全称 GRoup Outline Viewing Editor，我理解是个公司或者组织，它算是协同编辑算法研究的鼻祖之一吧。

GROVE 采用 Replicated Architecture。所有对共享文档的编辑操作一旦产生，就先在本地执行，之后广播到其它协同编辑者。这样所有协同编辑者都有共享文档的一份拷贝，没有单点。

如果每个协同编辑者收到其他人的编辑操作后不做任何改动就执行，会产生两个问题：Divergence 和 Causality-Violation。

Divergence：每个 Site 执行 Operation 的顺序不同。导致最终结果在各个 Site 之间不一致。

图1 上，Site 0 执行的 Operation 顺序为：O1, O2, O4, O3。 Site 1 执行顺序为: O2, O1, O3, O4 Site 2 执行顺序为：O2, O4, O3, O1

Causality -Violation：Operation 的执行顺序可能违反 Operation 的 Causal Order。

图1 上有 O1 -> O3，但是在 Site 2 上，O3 先于 O1 到达了 Site 2。于是 Site2 上如果每次收到 Operation 就立即执行，就会导致先执行了 O3，再执行 O1。Site2 上用户看到 O3 时候就会因为缺失 Context 而迷惑。

简单说就是：

可能 Operation 在各个 Site 执行顺序不同，导致各个 Site 上共享文本结果不一致；
Operation 执行顺序和产生顺序可能不同，违反 Causal Order。例如 A 编辑了两句话分别是 “我早上”， “吃了香蕉”。编辑消息在 B 上顺序变化导致 B 看到是 "吃了香蕉"，"我早上"。

提出并发正确标准

GROVE 在提出解决算法前，先提炼出协同编辑算法正确性标准，即协同编辑算法最终要达到的目标。

Convergence property。结束时，每个文档的拷贝都是相同的；
Precedence property。如果有 Oa -> Ob，则在所有 Site 上 Oa 一定先于 Ob 执行；

有了正确性判定的目标，GROVE 提出了协同编辑算法 distributed Operational Transformation 即 dOPT。但在介绍算法前，又有个概念，即什么是 Transformation。

变换函数

每次收到协同编辑的 Operation 不做改动就在本地执行是不行的。需要对收到的改动做一些变换，变换方法就称为变换函数。

dOPT 算法要求变换函数 T 必须满足：对于两个独立的 Operation Oa 和 Ob，如果 Oa' = T(Oa, Ob)，Ob' = T(Ob, Oa)，一定有：

C884DDE9-0253-488F-8900-BC77E4D1E30B-61185-000079B57E706FC1

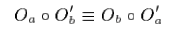
意思是说先执行 Oa 在执行变换后的 Ob，和先执行 Ob 再执行变换后的 Oa 结果相同，即如果执行前文档状态相同，两种不同方式执行下来文档的结果也相同。

除了 dOPT 明确写出来的对 T 的要求外，还有个隐含的要求是执行 T 的两个操作 Oa 和 Ob 是 non-serializable 的 (非串行？)。我个人理解就是 T 对 Oa 和 Ob 做完变换后得到的也只是一次操作。论文给的例子解释 non-serializable 是说比如 Oa 和 Ob 都在同一个位置做删除，T 做变换后不管是 Oa 先执行还是 Ob 先执行，在目标位置只能删除一个字符。即 Oa 和 Ob 本来都是删除一个字符操作，合并后也只是执行删除一个字符。

dOPT 算法

T 具体是什么是 application-dependent 的。即协同编辑算法 dOPT 并不关心 T 到底是什么样子。它只对 T 做一些 generic 的要求，只要 T 能满足要求，在这个协同编辑算法下就能达到前述协同编辑正确性目标。dOPT 的作用就是在记录了所有协同编辑 Operation 的前提下，每次收到一个 Operation 后根据历史记录选出需要根据 T 做变换的 Operation，决定变换执行顺序。

对于前面提出的协同编辑正确性目标，GROVE 给的解决办法里提出所有 Operations 都需要记录 Log，通过这个 Log 来解决 Precedence property 即给出两个 Operation 能判断出谁先谁后。dOPT 算法负责解决 Convergence property 即怎么样让 Operations 执行结果在各 Site 统一。

dOPT 描述如下。简单说就是每次收到一个 Operation O，就从 Log 内存储的历史 Operation 中找独立于当前 O 的这些 Operation 出来并用 T 做变换，最终将变换结果得到的 EO 写入 Log。需要知道 dOPT 实际并不会每收到一个 Operation 都跟自己历史记录里所有 Operation 都做一次变换，而是只对跟收到的 Operation 独立的记录做变换，而独立的 Operation 一定是有限数量的。不会每次都遍历所有历史记录。

dOPT(O, log) {
    EO = O;
    for (i = 1; i <= n; i++) {
        if (Log[i] || O)
        then EO = T(EO, Log[i]);
    }
    Execute EO;
    Append EO at the end of the Log;
}

dOPT 未解决的问题

13CE3349-A34E-42D1-BD1D-D3DA2CEB19D7-61185-00005ACAFBB9A88C

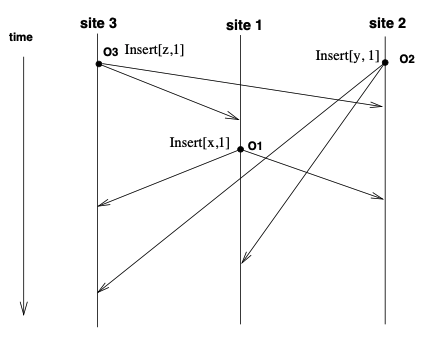
称为图 2。

举例说明 dOPT 没解决的问题。假设现在 Operation 是两个针对同一位置执行的插入操作，T 变换是按照 Operation 所属 site 编号来排优先级，编号低的插入操作会 shifted 即挪位置。例如 site 3 和 site1 都要对 1 号位做插入，那 T 变换后 site1 的插入位要改到 2 号位，site3 优先级高，能插入 1 号位。

按这个 T 变换执行 dOPT。

在 site 3 上，O3 先执行，得到 "z"。O1 收到后，因为 O3 -> O1，所以直接执行 O1 得到 "xz"，此时 Log 是 [O3, O1]。O2 收到后，O2 || O3 且 O2 优先级小于 O3 变换后得到 Insert[y, 2]，O2 || O1 且 O2 优先级大于 O1 得到 Insert[y, 2] 得到结果 "xyz"。

同理在 site1 上执行结果是，"xyz"。

在 site2 上，先执行 O2 得到 "y"，收到 O3 后和 O2 做变换，优先级比 O2 高，得到结果 "zy"，此时 Log 是 [O2, O3']。O3' 是做了变换的 O3。收到 O1 和 O2 做变换，得到 Insert[x, 2]，和 O3' 不做变换，得到结果 "zxy"。

注意：这里推导结果和论文里的不同，但也得出了三个 Site 不一致的结果。我觉得我推的是对的，所以按我的理解写。

看到并不是所有 site 上 dOPT 都一定能得出一致的结果。但如果把 T 的要求改一下，不是按照 site 编号大的优先级高，而是 site 编号小的优先级高，则图 2 中三个 Site 的结果都会是 "xyz" 是一致的。也就是说 dOPT 的正确性对 T 有要求，GROVE 后来还研究了很多种制定优先级的策略去保证 dOPT 的正确性。

REDUCE

REDUCE 跟随 GROVE 也是采用分布式和复制架构。用与 GROVE 里 Log 类似的称为 History Buffer (HB) 的东西记录所有执行过的 Operations。此外还引入了 Garbage Collection 机制从 HB 里去清理不再需要的 Operations。

Intention-violation

REDUCE 在 GROUP 提出的 Divergence 和 Causality-violation 问题之外，又提炼出一个新的协同编辑问题叫 Intention-Violation。

还是以上面的图 1 为例，为了方便起见再贴一次图 1。

0B8CF815-23B1-4369-A89D-F30D00EC1DBB-61185-00007D797F185617

图中 O1 和 O2 是独立的 Operation。在 Site 0 上，O2 是在 O1 执行完的基础上执行的，这就导致 O2 在 Site 0 上执行的 Context 和在 Site 1，Site 2 上执行时 Context 不一致，有所变化。

例如一开始是字符串 "ABCDE"，O1 = Insert["12", 2] 即想要修改为 "A12BCDE"。O2 = Delete[2,3] 即想要修改 "ABCDE" 为 "ABE" ，从 3 号位开始删掉 2 字符。因为 Context 不同，导致 Site 0 上执行结果会是 "A1CDE"，既不满足 O1 想要修改为 "A12BCDE" 的 Intention，也不满足 O2 想要修改为 "ABE" 的 Intention，按他们本来的目的 O1 和 O2 的预期结果是 "A12BE" 的。

注意 Intention-Violation 和 Divergence 不同。Divergence 通过增加串行执行机制就能避免，但是 Intention-Violation 即使加了串行机制也不行。比如在上面举例场景，即使加了 Operation 串行执行机制保证所有 Site 都是先执行 O1 再执行 O2，得到的结果依然是所有 Site 都是 "A1CDE"。依然不满足 O1 和 O2 的 Intention，只是说各 Site 执行结果统一了。

于是 REDUCE 在 GROVE 基础上又提出了新的协同编辑正确性指标：

Definition 3: A consistency model A cooperative editing system is consistent if it always maintains the following properties: 1. Convergence: when the same set of operations have been executed at all sites, all copies of the shared document are identical 2. Causality-preservation: for any pair of operations Oa and Ob, if Oa -> Ob, then Oa is executed before Ob at all sites; 3. Intention-preservation: for any operation O the effects of executing O at all sites are the same as the intention of O, and the effect of executing O does not change the effects of independent operations.

对于提出的三个问题，History Buffer (HB) 跟 GROVE 的 Log 一样负责解决 Causality-preservation。REDUCE 提出了一套 undo, do, redo 策略去解决 Convergence。用 Operational Transformation 算法来解决 Intention-preservation。

undo, do, redo

REDUCE 还提出三种新的 Operation，undo, do, redo 来解决 Convergence 问题。我们从提到的 Lamport Clock 里能知道，我们总是有办法能将分布式系统内所有事件的 Total Order 得到的。记为 =>，如 a => b 表示 a 事件在 b 事件之前。

REDUCE 要求 Operation 都必须有 Total Order，即能分辨出哪个 Operation 在前，哪个在后。Operation 执行顺序不一定严格按照 Total Order 进行，但必须按照 Causual Order 执行。比如 a => b => c 三个 Operation，这是他们的 Total Order。但执行时候执行完 a ，如果直接收到了 c，因为 a -> c，则 c 可以先执行，不满足 total order 但满足 Causual Order。最后收到 b 时直接执行就不满足 Causual Order 了，所以需要依赖 undo 先将 c undo 掉，再执行 b，再将 c redo。

通用的说，比如来了一个 Operation O： * 首先要执行 undo 。将当前 HB 内所有 Total Order 在 O 之后的 Operations 都 undo * 再执行 O ； * 最后执行 redo，将 HB 内本来在 O 后面被 undo 的 Operation 全部重来一遍

其中 undo 和 redo 是 REDUCE 提出的协同算法内部的 Operation，他们的执行中间结果不能暴露给用户。也很容易理解，不然比如用户就可能看到刚编辑的内容被删掉插了几个字后又出来，很诡异。

IT 和 ET

之前 GROVE 的问题是它对变换函数 T 有要求，T 不正确的时候 dOPT 不一定能满足 Convergence 条件，即可能出现各个协同端得到的结果不一致。(即前面介绍 dOPT 未解决的问题时，T 定义不同能得出不同结果) REDUCE 不依靠 T 来保证 Convergence，但它也有自己的要求。

REDUCE 区分出来了 Inclusion Transformation (IT) 和 Exclusion Transformation (ET)。

IT 是说 Oa 和 Ob 通过 T 做变换，得到的结果 Oa' 必须包含 Ob 的影响，此时 T 就称为 IT。它隐含的要求，做 IT 的两个 Operation 必须有相同的起始状态。即比如 site 1 上 History 是 O1, O2, O3，site 2 上文档的 History 是 O1, O2, O4，此时 site 1 收到 site 2 的 O4，这时候 O4 和 O3 能进行 IT 因为他们有相同的起始状态。如果 site 1 上 History 是 O1, O3。site 2 上是 O1, O2, O4。site 1 上收到 O4 后，O4 和 O3 就不能直接做 IT，因为它俩的起始状态不同。GROVE 的 dOPT 就没做这个区分也没 IT 的要求，收到什么操作都能做 T 变换，也不管 Context，所以有问题。

除了 IT 之外，为了应对 Intention-preservation，REDUCE 还引入了 ET。是说 Oa 和 Ob 做 ET 时，要排除 Ob 的影响。看文字很难理解，再把图 1 贴一遍如下。ET 的意思是说，比如 O4 到达 site 0 后，它并不能直接和 O1 做 Transformation，O4 得先对着 O2 做一次 ET 以排除 O2 的影响，得到 O4'。从而让 O4' 和 O1 拥有相同的 Document State 或者说 History，再让 O4' 和 O1 做 IT。

DD1E288B-C9AF-4C13-B8FD-9506368A2608-61185-00007FEFAAE8FCB5

Context

REDUCE 又定义了一个概念叫 Context。其含义就是 HB 内能从 Document 初始状态，一路执行 Operations 达到当前状态的 Operations 总和。

每个 Operation 有 Definition Context (DC) 记为 DC(O) 和 Execution Context (EC) 记为 EC(O) 两种 Context。对应 Operation 产生和实际被执行两个时间点。

为了做到 Intention-preservation，定义只有一个 Operation 的 DC(O) 和 EC(O) 相等的时候，就算作 Intention 被保留了。之前看到 Intention-preservation 问题介绍的时候是不是还挺疑惑的，感觉 Intention 似乎是个主观的不可被评价的东西，似乎不可能做到 Intention-preservation。但 REDUCE 这么通过 Context 来定义怎么去保留 Intention 就豁然开朗了。

因为 Context 就是一组 Operations 序列，所以 Context 除了是否相等外还有先后关系。比如 DC(Oa) 再多执行几个 Operation 后就能达到 DC(Ob) 则认为 Oa 的 context 在 Ob 之前。

论文里严格写下来是：

045873E7-506E-4B05-99AC-292EB44024B7-61185-0000810C571CF118

REDUCE 对 Transformation 的 pre/post 条件

前面提到 GROVE 对 Transformation 函数有限制条件，REDUCE 对 T 也会有所限制。REDUCE 将 Transformation 函数拆分出两种不同的 Transformation 即 IT 和 ET 记做 IT(Oa, Ob) 和 ET(Oa, Ob)。在有了 Context 的概念后，就能提出 REDUCE 对 Transformation 函数的限制条件：

BD8AF437-9185-4083-AD1C-7FDB0AB296CE-61185-0000814A5D20850B

即对 IT 来说，Pre 条件是 Oa Ob 必须有相同的 Define Context。IT 执行结果 Oa' 的 DC 要在 Ob 之后，且 Oa' 产生的效果要包含 Oa。

对 ET 来说 Pre 条件是 DC(Ob) 必须在 DC(Oa) 之前。执行结果 Oa' 要和 Ob 有相同 Define Context。我理解就是说 Oa' 是排除了 Ob 影响的 Oa 操作。比如 Ob 是在位置 1 插入 a，Oa 是在位置 2 插入 b，Ob -> Oa，结果是 ab。那排除 Ob 后的 Oa' 就是在位置 1 插入 b。

GOT

GOT 全名 Generic Operational Transformation。它是一个通过 IT，ET 实现的通用的 Transformation 函数。输入是一个 Operation 和 Operation 的 EC(O)，将 O 最终转化为 EO。且能满足 DC(EO) = EC(O)。

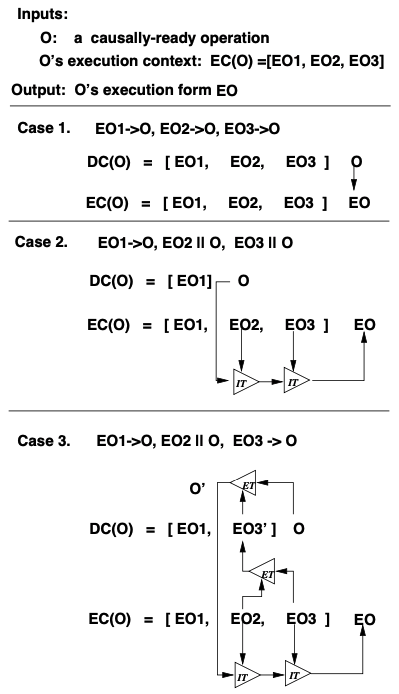
假设 EC(O) = HB = [EO1, EO2, EO3]。GOT 算法三种场景如下图，称为图 3：

E0108FD7-485A-42E3-8A30-75B29796BF22-61185-000082040060164E

有了前面内容后看这个图也就比较简单了。

Case1。O 在执行时候，Context 内所有 EO 都在 O 之前，都有 Causal Order。这种场景不需要做变换，直接执行 O。回想 dOPT 也是这样，非 Independent 的 Operation 先后顺序是明确的，不需要变换。
Case2。O 执行的时候在有 Causal Order 的 Operation 之后全都是 Independent Operation。例如图上 Case 2，O 执行时候从 EO1 这个有 Causal Order 的 Operation 之后的 EO2 和 EO3 与 O 都是 Independent 的。此时 O 和 EO2， EO3 都有共同的 Context，所以能直接连续执行 IT 得到 EO。
Case3。O 在执行的时候，在有 Causal Order 的 Operation 之后有 Independent Operation，接着又有至少一个有 Causal Order 的 Operation。因为 EO1 -> O，EO3 -> O，所以 DC(O) 中在 EO1 和 O 之间一定至少还有一个其它 Operation，记做 EO3'。这个 EO3' 和与当前 O 拥有 Independent 关系的 EO2 做了一次 Transformation 得到了 EO3。因为在执行 O 的时候已经拿不到 EC3' 了需要先根据 EO3 和 EO2 做一次 ET，得到 EO3’，再让 O 和 EO3' 做 ET 得到 O'，此时 DC(O') = DC(EO2)。所以 O' 和 EO2 能执行 IT，其结果又能与 EO3 执行 IT 最终得到 EO。

更严密的算法说明参看论文吧。

解决 dOPT 的问题

回头看 REDUCE 结合 undo, redo, do 和 GOT 解决 dOPT 之前的问题。重新贴图 2 如下。

我们假设有 Total Order O3 => O1 => O2。site3 和 1 不说了，得到的结果都是 "xzy"。只看 site2。

806AEE6B-2A78-4B70-B85A-E5A6BF07CCEE-61185-0000829442A65785

O2 先执行，得到 "y"。O3 到来，不满足 Causual Order，将 O2 undo，执行 O3 变成 "z"。再 redo O2，和 O3 做 IT(O2, O3)，得到 O2' = Insert[y, 2]，得到结果 "zy"。最后收到 O1，再次不满足 Causual Order，undo O2，do O1 得到 "xz"。再 redo IT(O2', O1) 得到 O2'' = Insert[y, 3]，最终结果为 "xzy"。

JUPITER

Jupiter 是 dOPT 上做优化而来。我们先看 Jupiter 算法，再看它和 dOPT 还有 GOT 有什么区别。Server 在本地处理完 Client 发来的 Operation 后将 Operation 广播至其它 Client。于是所有 Operation 只会来自两方，来自 Client 或来自 Server。来自 Server 的 Operation 意思是比如从另一个 Client B 发来的 Operation 在 Server 处理完后广播给 Client A 的。对 A 来说收到 B 的 Operation，这个 Operation 就是来自 B。

因为只有 Client 和 Server 两方，所以 Client 和 Server 的状态能通过二维图来表示。下图来自论文：High-Latency, Low-Bandwidth Windowingin the Jupiter Collaboration System。

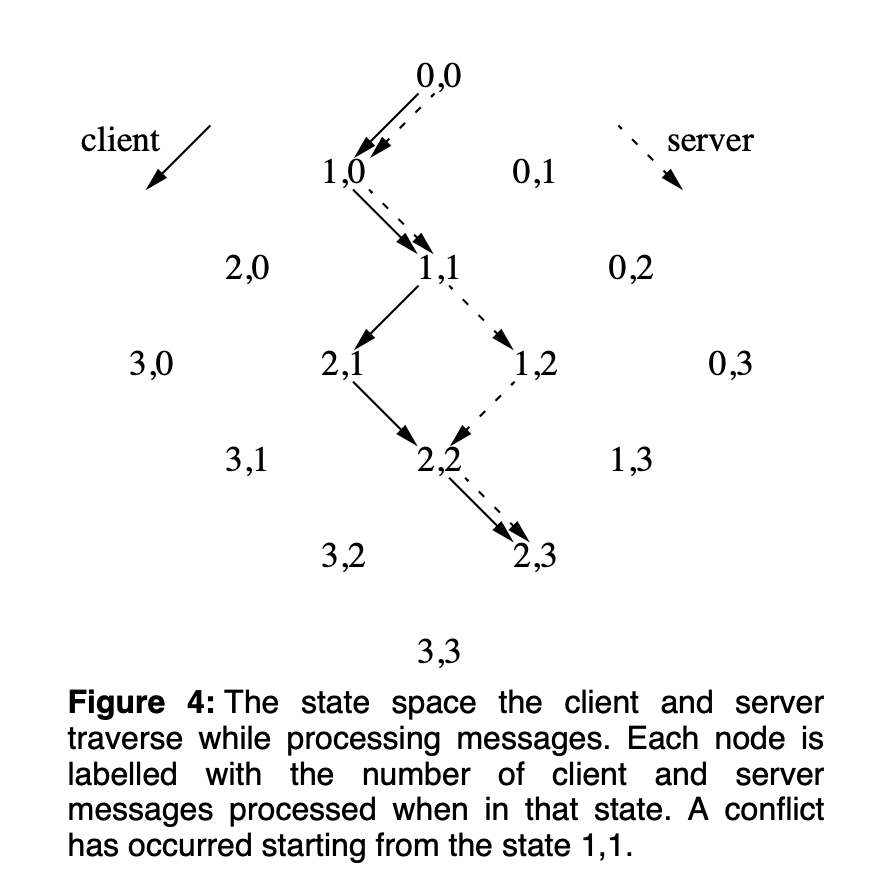
0553C190-7C49-47A1-A34D-E45713E075FB-61185-00014D36032DACA8

图上每个点位都是 Client 和 Server 可能达到的状态，每个边都是一个 Operation，实线是 Client 产生的 Operation 虚线是 Server 产生的 Operation。看到图中 Client 和 Server 开始在 0,0。Client 产生一个 Operation 自己处理后发给了 Server，Server 也处理后它俩都进入 1,0。之后 Server 收到其它 Client 的 Operation 也即认为 Server 自己产生了一个 Operation，Server 自己处理后发给 Client，于是它俩都进入 1,1。再往下，Client 产生一个 Operation 自己本地先处理后进入 2,1。Server 在还未收到 Client 的 Operation 时也产生一个 Operation，自己本地处理后发去 Client，Server 进入 1,2。这时候 Client 和 Server 的状态就出现了不一致。

Jupiter 称 OT 为 xform。当给定 Client 的一个 Operation c，一个 Server 的 Operation s，经过 xform 后能得到两个 Operation c' 和 s'，记为 xform(c, s) = {c', s'}。此后 Client 执行变换后的 s'，服务器执行变换后的 c' 就能保证 Client 和 Server 能进入相同的状态。

回到图中例子，Client 在 2,1，Server 在 1,2。让他俩产生分歧的 Operation 起始状态都是 1,1。将这两个产生分歧的 Operation 做 xform 或叫 OT 之后得到两个新的 Operation，被 Client 和 Server 分别执行后进入一致的 2,2 状态。之后 Server 又产生了一个 Operation，因为 Client 没冲突 Operation 产生，所以在 Client 和 Server 都执行新 Operation 后他们俩进入 2,3 这个状态。

那 xform 能举个例子不？

拿论文里的例子吧。比如 Client 和 Server 最初状态都是 "ABCDE"，Client 的 Operation x 是 del 4，即希望删除字母 D。Server 产生 Operation y 是 del 2，希望删除字母 B。那 xform(del 4, del2) = {del 3, del 2}。从 Client 侧来说，它在本地先执行 del 4 得到 "ABCE"，再执行 xform 的结果 del 2，得到 "ACE"。从 Server 侧来说，它在本地先执行 del 2 得到 "ACDE"，再执行 xform 的结果 del 3 得到 "ACE"。达到一致效果。

需要注意的是能做 xform 的 Operation 必须基于相同的状态，这就导致如果 Client 和 Server 之间差了不止一个 Operation，就需要特殊处理一下。比如下图，Server 连续产生了两个 Operation s1 和 s2，Client 产生了一个 Operation c。

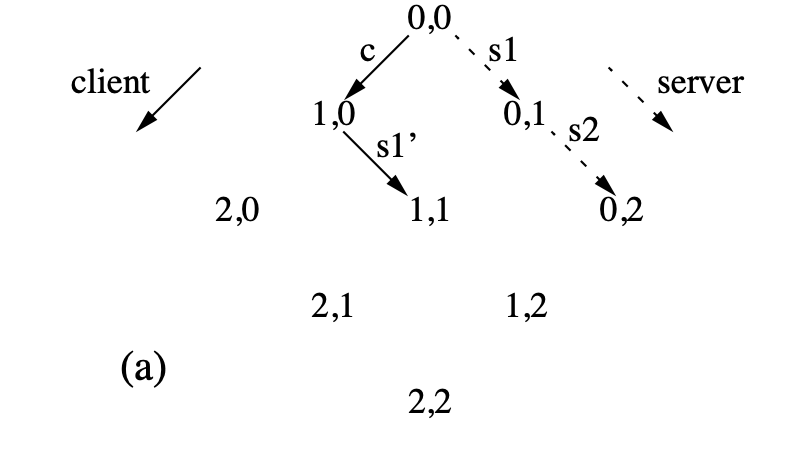
3346B07C-136A-4CBE-A045-810A81CB7EFC-61185-00014E967369DA56

c 可以和 s1 直接做 OT，得到 s1' 和 c'。但是 Client 即使执行了 s1' 也达不到 1,2 这个一致的状态。Server 执行了 c' 也只能达到 1,1 到不了 1,2。c 和 s2 也不能直接做 OT。

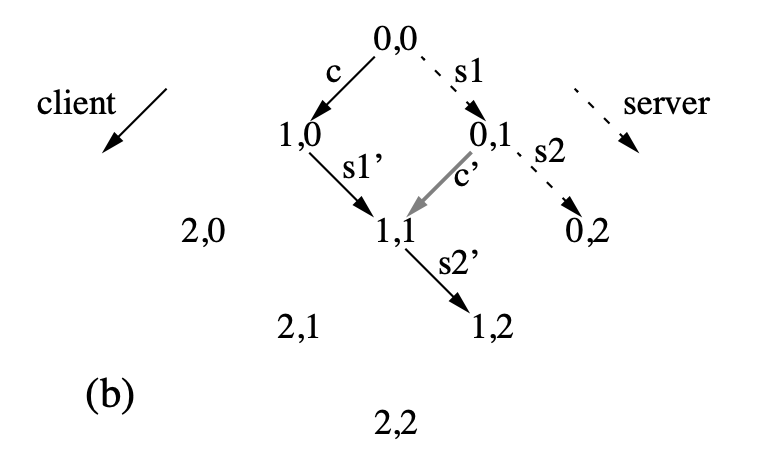
645E3F83-7088-428E-845A-31526C13DDE9-61185-00014EB776F961AD

解决办法是 c 和 s1 先做 OT 得到 c' 和 s1'。再让 c' 和 s2 做 OT 得到 s2' 和 c''。于是在 Client 上要先执行 c，再执行 s1' 和 s2'。在 Server 上执行完 s1, s2 后要执行 c' 就能达到一致的 1,2 状态。

也就是说不管是 Client 还是 Server，都需要记录对方的最新状态，或者说最新的 Operation 编号。比如 Client 每次产生 Operation 在本地执行完并发去 Server 后还需要在本地存着这个 Operation，直到收到 Server 的确认为止，才能将存储的 Operation 安全清除。再此期间 Client 需要记着这些 Operation 从而在收到 Server 的 Operation 后做 OT。同理 Server 也得这么干，但 Server 需要为所有 Client 保留他们的 Operation 编号，这也为 Jupiter 性能差留下了隐患。

Jupiter 算法最主要的部分就是这些，更详细的可以看论文。

个人觉得 Jupiter 最关键的就是在拓扑结构上的改造，即不是 N-Way 去做 OT，而是只有 Client 和 Server 双方。单这一点就压缩了产生冲突 Operation 的空间，从 N-Way 是 N 维的状态空间，压缩到了只有 Client Server 双方的 2-Way OT，即状态空间变成 2 维的了，所以才能直接将 Client Server 所有可能的状态在平面的纸上画出来，就像上面提的图一样。

这样从 Client 来说只需要维护两个计数，一个是自己发出 Operation 的计数，一个是 Server 发给 Client 的计数。每次发出 Operation 则 Client Operation 编号加一，收到 Server 发来的 Operation 时 Server 也会在里面带上这个 Operation 的编号。这样 Client 就能知道自己发出的 Operation 有哪些可能跟 Server 的 Operation 产生冲突，只存储这些可能产生冲突的 Operation，在未来做 OT。不可能产生冲突即 Server 已经处理过的 Operation 就能从自己本地安全的清理。不会像 dOPT 那样一直需要完整记录 Operation，不然比如理论上夸张点来说 A 用户永远不知道是不是有个用户 C 发出的 Operation 在一年后到达 A，从而 A 需要把这一年积累的 Operation 全部做一遍 OT。即对 Jupiter 来说，可能冲突的 Operation 是比较容易确定的。

另外，因为只有 Client 和 Server 两方，可能冲突的 Operation 又容易确定，也容易确定两个 Operation 是不是在相同 Context 下，能不能做 OT。而不用像 GOT 那样引入 IT，ET，undo，redo 等等概念和策略。大大简化了 OT 或者 xform 的难度。

唯一就是从 Server 来说性能差，需要为所有 Client 记录它们的 Operation 执行到哪里了，保留 Diverge 的 Operation，从而在收到它们的 Operation 能连续的做 OT 并把 Diverge 的 Operation 发给 Client 以达到最终一致的状态。

The ADOPTED APPROACH

下面内容配合着看「An Integrating, Transformation-Oriented Approach to Concurrency Control and Undo in Group Editors」这个论文的描述似乎更容易理解一些。

adOPTed 是在 GROVE 之上又做了改进。回顾 dOPT 对变换函数 T 的要求是：

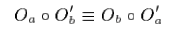
A51569E2-4018-4607-A643-AD79BD36171C-61185-000151E0E85DF9BF

称为 TP1，即当初始状态相同时起始状态进行 Oa，Ob' 两个 Operation 得到的结果与对起始状态进行 Ob，Oa' 两个 Operation 得到的结果相同。

Oa 和 Ob 一定是两个独立的 Operation，不然没必要做变化。可以将它俩看成正交的两条边，经过 T 变换生成的 Oa' 和 Ob' 与 Oa Ob 一起能组成一个矩形。借用「An Integrating, Transformation-Oriented Approach to Concurrency Control and Undo in Group Editors」里的图，Oa 和 Ob 在这个论文里对应的是 r1, r2:

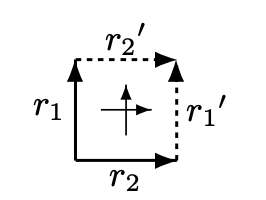
CEAC4179-9CC8-4896-B76A-77017D953745-61185-0001858C5AF1955C

每个顶点都是一个状态，每条边都是一个 Operation。r1 和 r2 是两个独立的 Operation，经过 T 变换后得到了 r1 和 r2 的对边，只有满足 TP1，在二维空间上 r1, r2' 到达的点才和 r2 r1' 到达的是同一个点，也即同一个状态，才能组成封闭的图形。

TP1 讲的是两个独立的 Operation 怎么通过 T 变化达成一致的方法，如果在此之上进一步拓展，来第三个 Operation r 后，因为 r 和 r1 r2 都独立，所以具象化的图形会从二维变换为三维：

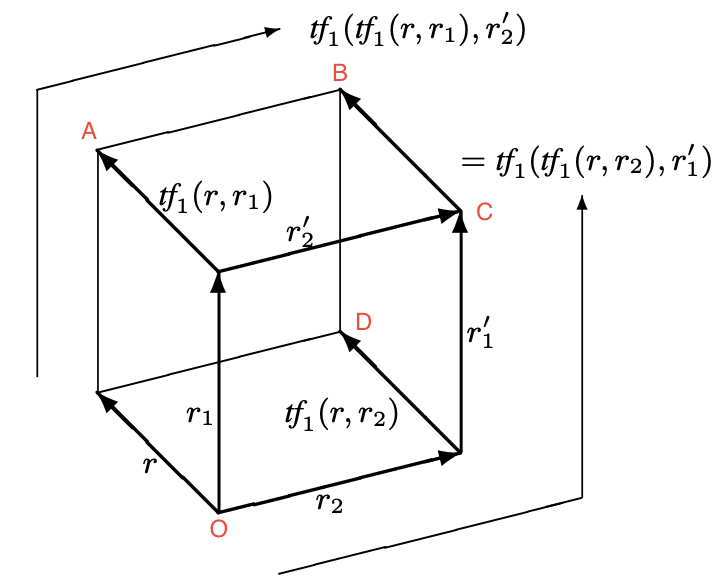
122B00C5-1F97-4C7D-BD6C-F8CD1F471752-61185-00018644397AEC1A

可以不管 tf1 是什么，就把它理解为之前的 T。没有本质区别。图上几个关键的顶点也即文档状态都被标记了字母。r1 是 site1 产生的 Operation，r2 是 site2 产生的 Operation。这个图先不看 r 只看 r1 和 r2，如果 T 满足了 TP1 的条件，那就能从起始 site1 和 site2 都一致的 O 状态，site1 通过 r1, r2' 两次 Operation，site2 通过 r2, r1' 两次 Operation，都能达到再次一致的状态 C。

现在来了 r 这个与 r1 和 r2 都独立且具有相同 Define Context 的 Operation。对 site1 来说，它需要连续的和 r1, r2' 做两次变换才能得到 E(r) 即执行态的 Operation。在 site2 来说 r 需要连续和 r2, r1' 做变换得到另一个执行态的 E2(r)。因为 r1, r2' 和 r2, r1' 都能达一致的 C 状态，所以有了 r 后 site1 和 site2 还能达到一致的状态 B，那就只能是要求 E(r) = E2(r)，也即 r 对 r1, r2' 连续做的两次变换得到的结果需要等于 r 对 r2, r1' 连续做两次变换得到的结果，就有了 TP2 即图上的 tf1(tf1(r, r1), r2') = tf1(tf1(r, r2), r1')。

我个人理解 TP1, TP2 的意义就是比如 Execution Context 内有 A B C 三个 Operation，将其中两个做变换得到的结果做交换 Execution Context 发生了变化但并不影响最终结果的状态。即 EC(A, B C) = EC(A, C', B') 其中 T(B, C) = (C', B')。

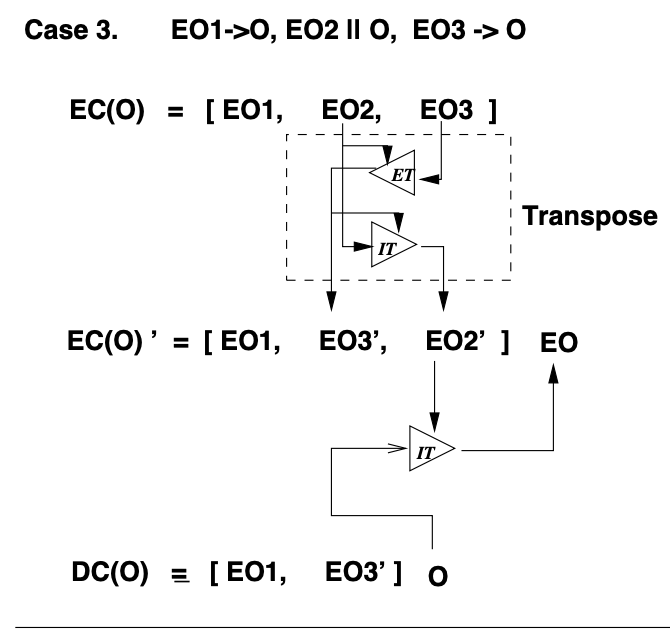
于是就有了对 GOT 的优化。GOT 内三种 Case 里能优化的只有 Case 3，再贴一遍 GOT 内的 Case 3：

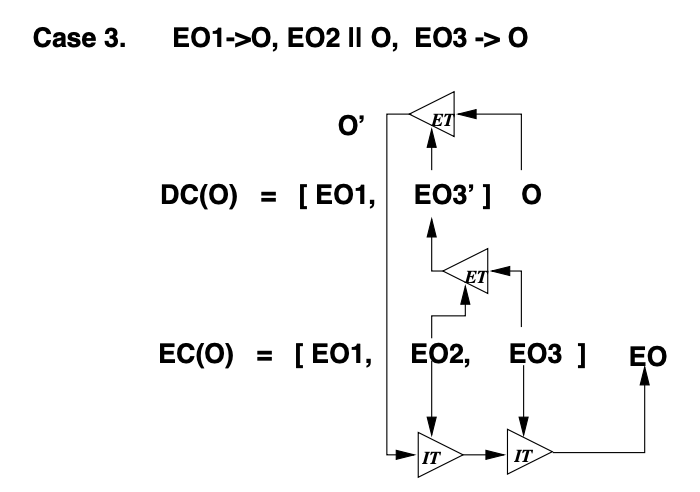
60DF91E2-0B04-42DD-BAD7-39243F26ACE2-61185-0001918B7DC87A1E

一共有四次操作，两次 ET，两次 IT。但如果变换满足 TP1 和 TP2 后，DC 内求 EO3' 方法保持原状，EO2， EO3 做 ET 得到。但是 EO2 和 EO3 通过变换能交换位置，得到的 EC(O)' 和 EC(O) 等效。这么交换之后，所有在 O 之前的操作和所有与 O 独立的操作分别在 EC(O)' 两边，不是混在一起了。这样一来因为 EC(O)' 和 DC(O) 除了 EO2' 外拥有相同的 Context，于是 EO2' 和 O 能直接做 IT 得到 EO。相对 GOT 少了一次 ET，所以得到了优化。

0CDE4B55-F6FD-42E8-9EBF-4A3BE742EBB3-61185-000191A13DB08AE8

参考

Operational Transformation in Real-Time Group Editors: Issues, Algorithms, and Achievements
Concurrenty Control in Groupware Systems
An Integrating, Transformation-Oriented Approach to Concurrency Control and Undo in Group Editors
Operational Transformation, the real time collaborative editing algorithm | Hacker Noon
http://www.codecommit.com/blog/java/understanding-and-applying-operational-transformation